JOB DESK IT SUPORT YANG HARUS ANDA KETAHUI

 

Ciri-Ciri Bangun Ruang

Secara umum, ciri-ciri atau sifat-sifat bangun ruang adalah sebagai berikut:

• Memiliki wajah atau sisi permukaan
• Memiliki tepi atau rusuk (tempat bertemunya sisi dengan sisi lainnya)
• Memiliki sudut
• Memiliki volume

 

Ciri yang disebut di atas juga dapat disebut sebagai unsur-unsur bangun ruang, atau karakteristik yang harus dimiliki suatu bangun untuk dapat disebut sebagai bangun ruang.

Baca Juga: Kedudukan Titik, Garis, dan Bidang pada Bangun Ruang

 

Rumus Luas dan Volume Bangun Ruang

Berikut rumus-rumus bangun ruang berdasarkan masing-masing jenisnya. Simak baik-baik, ya!

 

1. Rumus Luas dan Volume Kubus

Kubus adalah bangun ruang yang memiliki enam sisi berbentuk persegi yang sama besar. Semua rusuk pada kubus memiliki panjang yang sama.

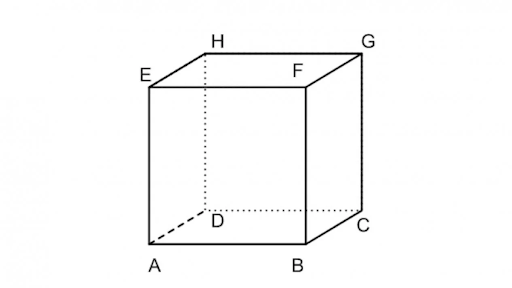
Gambar Kubus (Sumber: thumb.viva.co.id)

 

Ciri-Ciri Kubus

• Memiliki 12 rusuk yang panjang sama.
• Memiliki 6 sisi berbentuk persegi.
• Memiliki 8 titik sudut.
• Memiliki 12 diagonal sisi atau diagonal bidang.
• Memiliki 4 diagonal ruang.
• Memiliki 6 bidang diagonal.
• Memiliki 3 pasang bidang sejajar yang sama dan sebangun.

 

Rumus Luas Permukaan Kubus

Luas Permukaan = 6 × sisi × sisi 

L = 6 × s2

 

Rumus Volume Kubus

Volume = sisi × sisi × sisi 

V = s3

 

Contoh Soal:

Sebuah kubus memiliki panjang sisi 4 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui: s = 4 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan kubus

L = 6 × s2

L = 6 × 42

L = 6 × 16 = 96 cm²

Jadi, luas permukaan kubus tersebut adalah 96 cm².

 

b. Volume kubus

V = s3

V = 43

V = 64 cm³

Jadi, volume kubus tersebut adalah 64 cm³.

 

2. Rumus Luas dan Volume Balok

Sama seperti kubus, balok adalah bangun ruang yang memiliki enam sisi, namun sisi-sisinya berbentuk persegi panjang. Tiga pasang sisi balok yang berhadapan akan sama besar.

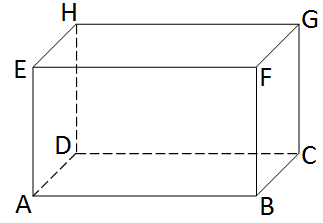
Gambar Balok (Sumber: Ruangguru.com)

 

Ciri-Ciri Balok

• Memiliki 6 buah sisi.
• Memiliki 12 rusuk.
• Memiliki 12 diagonal bidang.
• Memiliki 8 titik sudut.
• Memiliki 4 diagonal ruang.
• Memiliki 6 bidang diagonal.
• Memiliki luas permukaan dan volume.

 

Rumus Luas Permukaan Balok

Luas Permukaan = 2 × ((panjang × lebar) + (panjang × tinggi) + (lebar × tinggi))

L = 2 × ((p × l) + (p × t) + (l × t))

 

Rumus Volume Balok

Volume = panjang × lebar × tinggi

V = p × l × t

 

Contoh Soal:

Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui: p = 8 cm, l = 4 cm, t = 6 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan balok

L = 2 × ((p × l) + (p × t) + (l × t))

L = 2 × ((8 × 4) + (8 × 6) + (4 × 6)) 

L = 2 × (32 + 48 + 24) = 208 cm²

Jadi, luas permukaan balok tersebut adalah 208 cm².

 

b. Volume balok

V = p × l × t

V = 8 × 4 × 6 = 192 cm³

Jadi, volume balok tersebut adalah 192 cm³.

Baca Juga: Macam-Macam, Sifat & Rumus Bangun Segi Empat 

 

3. Rumus Luas dan Volume Limas

Selanjutnya, limas adalah bangun ruang yang memiliki alas berbentuk segitiga, segiempat, segilima, segienam, dan seterusnya (segi-n), dan sisi-sisi tegak berbentuk segitiga yang bertemu di satu titik puncak.

Jika alas limas berbentuk segitiga, maka bangun tersebut disebut limas segitiga. Jika alasnya berbentuk segiempat, maka disebut limas segiempat, begitupun dengan limas segilima, limas segienam, dan seterusnya.

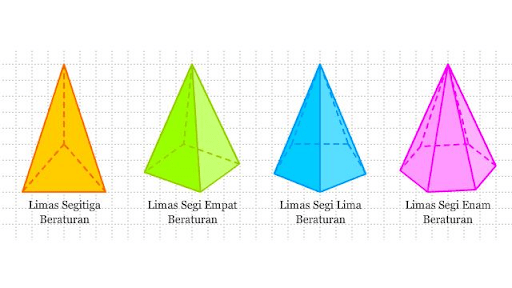
Gambar Limas (Sumber: Popmama.com)

 

Ciri-Ciri Limas

• Memiliki 7 titik sudut.
• Memiliki 12 rusuk.
• Memiliki 6 sisi tegak.
• Memiliki 1 sisi alas.
• Mempunyai sisi tegak berbentuk segitiga.
• Sisi alasnya berbentuk segi banyak.
• Mempunyai satu titik puncak.
• Penamaan limas tergantung bentuk alasnya.

 

Rumus Luas Permukaan Limas

Luas Permukaan = Luas alas + Luas selimut

L = Lalas + Lselimut

 

Rumus Volume Limas

Volume = 1/3 × Luas alas × tinggi limas

V = 1/3 × Lalas × t

 

Keterangan:

• Luas alas limas, rumusnya tergantung pada bentuk alas limas. Misalnya, pada limas segiempat, luas alasnya = p x l.
• Luas selimut​ adalah luas sisi-sisi tegak limas. Karena sisi-sisi tegak limas berbentuk segitiga, maka Lselimut​ = 1/3 × panjang alas × t.

 

Contoh Soal:

Sebuah limas persegi memiliki panjang sisi alas 5 cm dan tinggi 10 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

p = 5 cm

t = 10 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan limas

L = Lalas + Lselimut

Kita cari luas alas dan luas selimutnya satu per satu, ya!

• Luas alas

Karena alas limas tersebut berbentuk persegi, jadi untuk mencari luas alas, kita menggunakan rumus mencari luas persegi.

L = s2 = 52 = 25 cm²

• Luas selimut
  

Kemudian, untuk luas selimut, kita bisa gunakan luas segitiga, yaitu:

L = ½ × a × t

L = ½ × 5 × 10 = 25 cm²

Setelah kita mendapatkan luas alas dan luas selimutnya, barulah kita bisa mencari luas permukaan limas.

L = Lalas + Lselimut

L = 25 + 25 = 50 cm²

Jadi, didapat luas permukaan limas persegi tersebut adalah 50 cm².

 

b. Volume limas

V = 1/3 × Lalas × t

V = 1/3 × 25 × 10 = 83,33 cm³

Jadi, volume limas persegi tersebut adalah 83,33 cm³.

 

4. Rumus Luas dan Volume Prisma

Prisma adalah bangun ruang yang memiliki dua alas sejajar dan kongruen, serta sisi tegak yang berbentuk segi empat. Sama seperti limas, prisma diberi nama berdasarkan bentuk alasnya. Kalo alasnya berbentuk segitiga, maka namanya prisma segitiga, begitupun seterusnya.

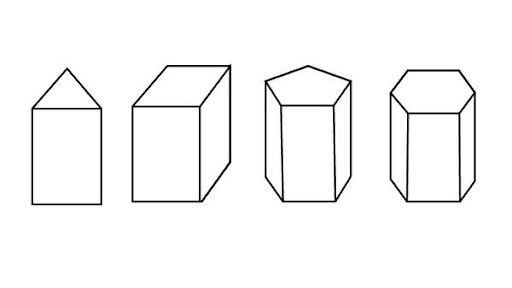
Gambar Prisma (Sumber: Popmama.com)

 

Ciri-Ciri Prisma

• Memiliki alas, tutup, dan selimut.
• Selimut prisma merupakan bidang datar, bisa kotak ataupun persegi panjang.
• Memiliki sudut sebanyak 2 kali segi alasnya.
• Memiliki rusuk 3 kali segi alasnya.
• Memiliki ujung-ujung yang identik satu sama lain.

 

Rumus Luas Permukaan Prisma

Luas Permukaan = (2 × Luas alas) + Luas selimut

L = (2 × Lalas) + Lselimut

L = (2 × Lalas) + (Kalas × t)

 

Rumus Volume Prisma

Volume = Luas alas × tinggi prisma

V = Lalas × t

Keterangan:

• Luas alas prisma, rumusnya tergantung pada bentuk alas prisma. Misalnya, pada prisma segiempat, luas alasnya = p x l.
• Luas selimut​ adalah luas sisi-sisi tegak prisma. Kita bisa mencarinya dengan rumus keliling alas × tinggi.
• Rumus volume prisma segiempat maupun segi lainnya, dihitung menggunakan rumus volume prisma secara umum.

 

Contoh Soal:

1. Sebuah prisma segitiga siku-siku memiliki panjang sisi alasnya 3 cm, 4 cm, dan 5 cm. Jika tinggi prisma adalah 6 cm, berapakah luas permukaan prisma tersebut?

 

Pembahasan:

L = (2 × Lalas) + (Kalas × t)

Kita cari luas alas dan keliling alasnya dulu, ya. Karena alas prisma berbentuk segitiga siku-siku, maka luas alasnya bisa kita cari menggunakan rumus:

L = ½ × a × t

L = ½ × 3 × 4 = 6 cm²

Kemudian, untuk keliling alas, kita bisa cari dengan menghitung jumlah sisi-sisi segitiga:

Kalas = sisi + sisi + sisi = 3 + 4 + 5 = 12 cm

Sehingga, luas permukaan prismanya adalah:

L = (2 × Lalas) + (Kalas × t)

L = (2 × 6) + (12 × 6)

L = 12 + 72 = 84 cm²

Jadi, luas permukaan prisma segitiga tersebut adalah 84 cm².

 

2. Sebuah prisma segitiga memiliki luas alas 20 cm² dan tinggi prisma 12 cm. Hitunglah volumenya!

 

Pembahasan:

V = Lalas × t

V = 20 × 12 = 240 cm³

Jadi, volume prisma segitiga tersebut adalah 240 cm³.

Baca Juga: Cara Menghitung Luas Permukaan dan Volume Gabungan Bangun Ruang Sisi Lengkung

 

5. Rumus Luas dan Volume Bola

Bola adalah bangun ruang yang seluruh permukaannya berjarak sama dari titik pusatnya. Karena termasuk bangun ruang sisi lengkung, maka bola tidak memiliki sisi datar.

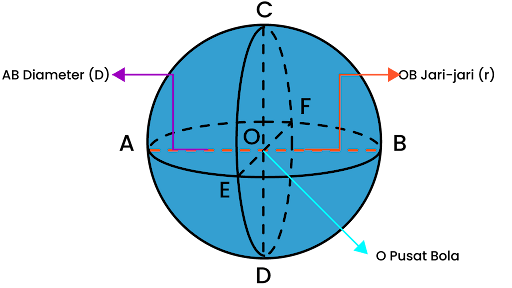
Gambar Bola (Sumber: Ruangguru.com)

 

Ciri-Ciri Bola

• Tidak memiliki rusuk dan titik sudut.
• Memiliki satu bidang sisi lengkung, yakni selimut bola.
• Terdapat jari-jari dan diameter.
• Memiliki luas permukaan dan volume.

 

Rumus Luas Permukaan Bola

Luas Permukaan = 4 × π × (jari-jari bola)2

L = 4 × π × r2

 

Rumus Volume Bola

Volume = 4/3 × π × (jari-jari bola)3

V = 4/3 × π × r3

 

Rumus Volume Setengah Bola

Volume = 2/3 × π × jari-jari bola

V = 2/3 × π × r

 

Catatan: Nilai π bisa 22/7 atau 3,14, tergantung yang diketahui di soal.

 

Contoh Soal:

Sebuah bola memiliki jari-jari 7 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

a. Luas permukaan bola

L = 4 × π × r2

L = 4 × 22/7 × 72 

L = 4 × 22/7 × 49 = 616 cm²

Jadi, luas permukaan bola tersebut adalah 616 cm².

 

b. Volume bola

V = 4/3 × π × r3

V = 4/3 × 22/7 × 73 

V = 4/3 × 22/7 × 343 = 1.436 cm³

Jadi, volume bola tersebut adalah 1.436 cm³.

Baca Juga: Rumus Luas dan Volume Bola, Cara Menghitung & Contohnya

 

6. Rumus Luas dan Volume Kerucut

Kamu pernah menggunakan topi ulang tahun? Nah, topi ulang tahun itu bentuknya seperti kerucut, loh. Secara definisi, kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan sisi tegak yang melengkung dan bertemu di satu titik puncak.

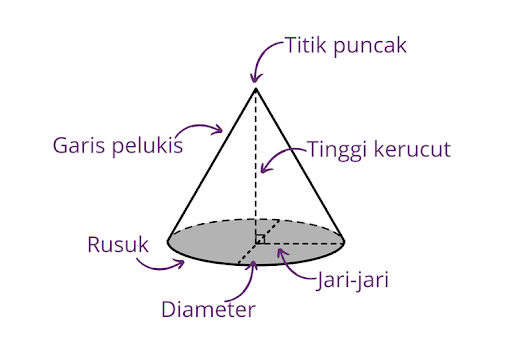
Gambar Kerucut (Sumber: Kompas.com)

 

Ciri-Ciri Kerucut

• Mempunyai 2 sisi berbentuk lingkaran dan melengkung.
• Sisi lingkaran merupakan alas, dan sisi melengkung sebagai selimut.
• Mempunyai 1 rusuk berbentuk bulat.
• Mempunyai 1 sudut di ujung kerucut.

 

Rumus Luas Permukaan Kerucut

Luas Permukaan = π × jari-jari alas × (jari-jari alas + garis pelukis)

L = π × r × (r + s)

 

Rumus Volume Kerucut

Volume = 1/3 × π × (jari-jari alas)2 × tinggi kerucut

V = 1/3 × π × r2 × t

 

Rumus Garis Pelukis Kerucut

 

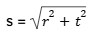
Contoh Soal:

Sebuah kerucut memiliki jari-jari alas 5 cm dan tinggi 12 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

r = 5 cm

t = 12 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan kerucut

L = π × r × (r + s)

Pertama-tama, kita cari garis pelukis kerucutnya terlebih dahulu, ya:

Sehingga, garis pelukis kerucut tersebut adalah 13 cm. Dengan begitu, kita bisa mencari luas kerucutnya dengan cara:

L = π  ×  r  ×  (r  +  s)

L = 22/7 × 5 × (5 + 13) 

L = 22/7 × 5 × 18 = 282,74 cm²

Jadi, luas permukaan kerucut tersebut adalah 282,74 cm².

 

b. Volume kerucut

V = 1/3 ×  π  ×  r2 × t

V = 1/3 × 22/7 × 52 × 12 = 314 cm³

Jadi, volume kerucut tersebut adalah 314 cm³.

Baca Juga: Rumus Luas & Volume Kerucut serta Contoh Soalnya

 

7. Rumus Luas dan Volume Tabung

Kalo ngomongin tabung, pasti banyak di antara kamu yang udah kebayang bentuknya, ya. Tabung adalah bangun ruang yang memiliki alas dan tutup berbentuk lingkaran yang sama besar, serta sisi tegak yang berbentuk persegi panjang melingkar. Contohnya kayak dirigen minyak, nih.

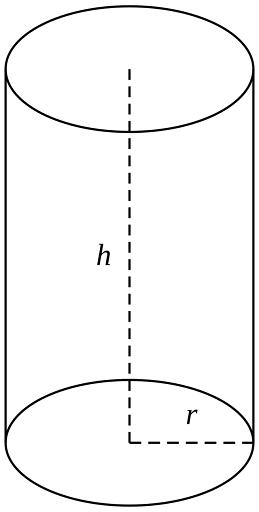
Gambar Tabung (Sumber: Wikimedia.org)

 

Ciri-Ciri Tabung

• Memiliki 2 rusuk.
• Memiliki 3 sisi, yaitu 2 sisi berbentuk lingkaran dan 1 sisi lengkung.
• Tinggi tabung adalah jarak antara alas dengan tutup tabung.
• Sisi alas serta tutupnya berbentuk lingkaran dan sama besar.
• Tidak memiliki titik sudut.

 

Rumus Luas Permukaan Tabung

Luas Permukaan = 2 × π × jari-jari alas × (jari-jari alas + tinggi tabung)

L = 2 × π × r × (r + t)

 

Rumus Volume Tabung

Volume = π × (jari-jari alas)2 × tinggi tabung

V = π × r2 × t

 

Contoh Soal:

Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan dan volumenya!

 

Pembahasan:

Diketahui:

r = 7 cm

t = 10 cm

Ditanya: L dan V …?

Jawab:

a. Luas permukaan tabung

L = 2 × π × r × (r + t)

L = 2 × 22/7 × 7 × (7 + 10) 

L = 2 × 22/7 × 7 × 17  = 748 cm²

Jadi, luas permukaan tabung tersebut adalah 748 cm².

 

b. Volume tabung

V = π × r2 × t

V = 22/7 × 72 × 10

V = 22/7 × 49 × 10 = 1.540 cm³